دانلود با لینک مستقیم و پر سرعت .

مقدمه
هندسه تحلیلی شامل مباحثی چون بردارها ، معادلات حرکت پرتابه ، معادلات خط ، ضرب عددی و برداری، بردارها. مقاطع مخروطی که در هندسه یونان پا گرفت و امروزه با معادلات درجه دو بعنوان منحنیهایی در صفحه مختصات توصیف میشوند یونانیان زمان افلاطون این منحنیها را فصل مشترک یک صفحه با یک مخروط میگرفتند که نام مقطع مخروطی از آن ناشی شده است. نکتهای که حائز اهمیت اشاره به این مسئله است که در مطالعات هندسه تحلیلی مختصات دکارتی از اهمیت فوقالعادهای دارد زیرا توسط این مختصات ما میتوانیم طول و عرض و ارتفاع اجسامی را که میبینیم به صفحه منتقل کرده و درباره آنها براحتی به مطالعه پردازیم.
بردارها
برخی از کمیات که اندازه میگیریم با اندازهشان کاملا مشخص میشوند مانند جرم ، طول ، زمان. اما همانطور که میدانیم توصیف یک نیرو ، تغییر مکان و سرعت تنها با اندازه مشخص نمیشوند بلکه برای درک صحیحی از آنها باید جهت آنها نیز برای ما مشخص باشند کمیاتی که علاوه بر اندازه دارای جهت نیز میباشند معمولا با پیکانهایی به نمایش درمیآیند که به جهت اثر کمیت اشاره میکنند و طولهایشان به اندازه اثر آنها برحسب واحد مشخص اشاره میکنند. به این کمیات بردار میگوییم.
یک بردار واقع در صفحه عبارت است از پارهخطی جهتدار از آنجا که بردار اساسا از طول و جهت تشکیل میشود و بردار را همسنگ و یا حتی یکی مینامیم هرگاه طول و جهتشان یکی باشد.
بردارهای نوین امروزی ریشه در کواترنیونها دارند. کواترنیونها تعمیمی هستند از جفت  به چهارتایی مرتب
به چهارتایی مرتب  . جبر کواترنیونها را ویلیام همیلتن ریاضیدان ایرلندی (1805-1865) ابداع کرد. اما مهندسان علیالخصوص اولیور هویساید آنالیز برداری را رواج دادند. برخی از فیزیکدانان از جمله شاخصترین آنها جیمز کلارک ماکسول ، از هر دو مضمون کواترنیونها و بردارها بهره بردند. سرانجام مقارن با تحویل قرن ، آنالیز برداری گیبس و هوسیاید غلبه کرد. مهندسان از جمله نخستین معتقدان، فیزیکدانان از نخستین گروندگان و ریاضیدانان آخرین پذیرندگان این باب از ریاضیات بودند.
. جبر کواترنیونها را ویلیام همیلتن ریاضیدان ایرلندی (1805-1865) ابداع کرد. اما مهندسان علیالخصوص اولیور هویساید آنالیز برداری را رواج دادند. برخی از فیزیکدانان از جمله شاخصترین آنها جیمز کلارک ماکسول ، از هر دو مضمون کواترنیونها و بردارها بهره بردند. سرانجام مقارن با تحویل قرن ، آنالیز برداری گیبس و هوسیاید غلبه کرد. مهندسان از جمله نخستین معتقدان، فیزیکدانان از نخستین گروندگان و ریاضیدانان آخرین پذیرندگان این باب از ریاضیات بودند.
بردارها درفضا
مهمترین ویژگی بردارها در فضا مانند حالتی که در صفحه داشتند طول و جهت آنهاست. طول برداری مانند  با دوبار استفاده از قضیه فیثاغورث بدست میآید. و جهت آنها از تقسیم مولفههای برداری چون A بر اندازهاش بدست میآید.
با دوبار استفاده از قضیه فیثاغورث بدست میآید. و جهت آنها از تقسیم مولفههای برداری چون A بر اندازهاش بدست میآید.
معادلات پارامتری حرکت ایدهآل پرتابه
برای بدست آوردن معادلات حرکت پرتابه فرض میکنیم پرتابه مانند ذرهای رفتار میکند که در صفحه مختصات قائم حرکت میکند و تنها نیروی موثر بر آن در ضمن حرکتش ، نیروی ثابت گرانش است که همواره روبه پایین است. در عمل هیچ یک از این فرضیات برقرار نیست زمین در زیر پرتابه میچرخد هوا نیروی اصطکاکی ایجاد میکند که به سرعت و ارتفاع پرتابه بستگی دارد. برای توصیف حرکت در یک دستگاه مختصات مشخص فرض میکنیم پرتابه در لحظه 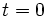 از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه
از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه 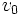 است و بردار سرعت با محور xxهای مثبت زاویه
است و بردار سرعت با محور xxهای مثبت زاویه  میسازد. در هر لحظه t ،
میسازد. در هر لحظه t ، 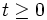 ، مکان پرتابه با جفت مختصات
، مکان پرتابه با جفت مختصات 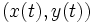 . مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد:
. مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد:
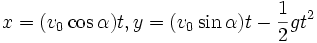
مسیر ایدهآل یک سهمی است.
اغلب ادعا میشود که مسیر حرکت آبی که از یک لوله بیرون میجهد یک سهمی است اما اگر به دقت این مسیر بنگریم میبینیم که هوا سقوط آب را کند میکند و حرکت آن رو به جلو آنقدر کند است که از انتهای سقوطش از شکل سهموی خارج میشود. ادعایی که در مورد سهموی بودن حرکت میشود فقط در مورد پرتابههای ایدهآل واقعا درست است. این مطلب را میتوان از روابط که در بالا برای y ,x ذکر شد بدست آورد. بدین ترتنیب که هرگاه مقدار t را از معادله x بدست آوردیم و آن را در معادله y جاگذاری کنیم معادله دکارتی بدست آمده نسبت به x از درجه دوم و نسبت به y از درجه اول است پس نمودارش یک سهمی است.
خط در فضا
فاصله در فضا
گاهی لازم است که فاصله بین دو نقطه مثل 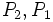 در فضا مشخص باشد برای این کار طول
در فضا مشخص باشد برای این کار طول  را مییابیم که در اینصورت داریم:
را مییابیم که در اینصورت داریم:
وسط پاره خط
مختصات نقطه وسط M پارهخطی که دو نقطه 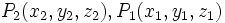 را بهم وصل میکند متوسط مختصات
را بهم وصل میکند متوسط مختصات 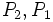 هستند. برای پیبردن به دلیل این مطلب کافی است توجه کنیم که این نقطه مختصات مولفه عددی برداری است که مبدا را به MM وصل میکند که به این ترتیب تمام مولفههای M از نصف مجموع مولفههای نظیر به نظیر
هستند. برای پیبردن به دلیل این مطلب کافی است توجه کنیم که این نقطه مختصات مولفه عددی برداری است که مبدا را به MM وصل میکند که به این ترتیب تمام مولفههای M از نصف مجموع مولفههای نظیر به نظیر 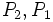 بدست میآید.
بدست میآید.
زوایای بین خمها
زوایای بین دو خم مشتقپذیر در یک نقطه تقاطع آنها عبارتاند از زوایای بین خطهای راس بر آنها در آن نقطه.
معادلههای خط و پارهخط
فرض میکنیم L خطی باشد در فضا که از نقطه  بگذرد و موازی با بردار
بگذرد و موازی با بردار 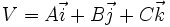 باشد. پس L مجموعه نقاطی است مانند
باشد. پس L مجموعه نقاطی است مانند  به قسمی که بردار
به قسمی که بردار  با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند tt داشته باشیم:
با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند tt داشته باشیم: 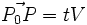 این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از:
این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از:
وقتی پارامتر t از 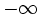 تا
تا 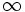 افزایش مییابد نقطه
افزایش مییابد نقطه  دقیقا یکبار خط را میپیماید. وقتی t بازه بسته
دقیقا یکبار خط را میپیماید. وقتی t بازه بسته 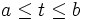 را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود.
را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود.
فاصله یک نقطه از یک خط
برای یافتن نقطهای چون P از خطی مانند L کافی است برای اولین قدم نقطهای مانند Q را روی L در نظر بگیریم که نزدیکترین فاصله را تا P داشته باشد سپس برای قدم دوم لازم است فاصله P تا Q را محاسبه کنیم بدین ترتیب فاصله یک نقطه از خط دیگری را بدست آوردهایم.
معادله صفحه
فرض میکنیم M معرف صفحهای از فضاست که از نقطه  میگذردو بر بردار ناصفر
میگذردو بر بردار ناصفر 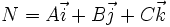 عمود است. پس M از مجموعه نقاطی مانند
عمود است. پس M از مجموعه نقاطی مانند  تشکیل میشود که به ازای آنها بردار
تشکیل میشود که به ازای آنها بردار  بر N عمود است. یعنی P روی MM است اگر و تنها اگر:
بر N عمود است. یعنی P روی MM است اگر و تنها اگر: 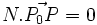
با جاگذاری عبارت معادل در تساوی فوق معادله صفحه حاصل میشود.
زاویه بین دو صفحه ، فصل مشترک دو صفحه
بنابه تعریف زاویه بین دو صفحه متقاطع ، زاویه حادهای است که دو بردار قائم بر آنها با هم میسازند. بنابراین زاویه بین دو صفحه  که بردارهای
که بردارهای  قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود:
قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود:
(منظور از | | ، اندازه بردارها میباشد.)
برای یافتن معادلات پارامتری فصل مشترک دو صفحه ابتدا برداری موازی با فصل مشترک و سپس نقطهای واقع بر فصل مشترک مییابیم. همانطور که میدانیم هر بردار که موازی با فصل مشترک دو صفحه باشد با هر دو صفحه مفروض موازی است لذا بر بردارهای قائم بر آن دو صفحه عمود است. بنابراین با یافتن بردار حاصل ضرب خارجی بردارهای عمود بر صفحات میتوان بردار موازی فصل مشترک را بیابیم. برای یافتن نقطهای روی فصل مشترک باید نقطهای بیابیم که در هر دو صفحه باشد بدین منظور z=0 را در معادلات صفحه قرار میدهیم و دستگاه حاصل را نسبت به x , y حل میکنیم نقطه حاصل در هر دو صفحه خواهد کرد.
کاربردها
هندسه تحلیلی همانطور که از نامش پیداست به تحلیل و کنجکاوی هندسه و روابط هندسی میپردازد و کاربردهای آن در مسیر علوم از جمله فیزیکی -اخترشناسی- هوافضا- حتی شیمی غیرقابل انکار است. همه مطالب ذکر شده فوق مقدمهای است برای بررسی مفصلتر حرکت. مبحث بردارها پایه خوبی برای بسط و گسترش حساب دیفرانسیل و انتگرال فراهم آورده است.
فهرست مطالب:
بردار در صفحه
فاصله دو نقطه از هم
طول بردار
مثال
بردار همسنگ
جمع دو بردار
تفریق دو بردار
ضرب عدد در بردار
ویژگی های ضرب عدد در بردار
بردار یکه
تصویر بردار
مثال
مختصات فضایی
فاصله دو نقطه در فضا
تعریف کره
معادله کره
بردارهای فضایی
مثال
زاویه بین دو بردار
ضرب داخلی
مثال
نابرابری کوشی-شوارتس
تصویر بردارها
مثال
خط در صفحه و در فضا
کسینوس های هادی
مثال
بردارهای موازی
معادلات خط در فضا
مثال
دو خط متنافر
معادله صفحه
مثال
زاویه بین دو صفحه
فاصله یک نقطه از یک صفحه
مثال
ضزب خارجی بردارها
مثال
تعبیر هندسی ضرب خارجی
مساحت مثلث
حجم متوازی السطوح
فاصله یک نقطه از یک خط
عمود مشترک دو خط متنافر
و...





 به چهارتایی مرتب
به چهارتایی مرتب  . جبر کواترنیونها را
. جبر کواترنیونها را  با دوبار استفاده از
با دوبار استفاده از 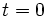 از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه
از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه 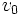 است و بردار سرعت با محور xxهای مثبت زاویه
است و بردار سرعت با محور xxهای مثبت زاویه  میسازد. در هر لحظه t ،
میسازد. در هر لحظه t ، 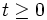 ، مکان پرتابه با جفت مختصات
، مکان پرتابه با جفت مختصات 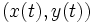 . مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد:
. مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد: 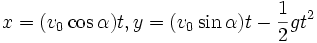
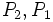 در فضا مشخص باشد برای این کار طول
در فضا مشخص باشد برای این کار طول  را مییابیم که در اینصورت داریم:
را مییابیم که در اینصورت داریم:
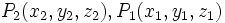 را بهم وصل میکند متوسط مختصات
را بهم وصل میکند متوسط مختصات  بگذرد و موازی با بردار
بگذرد و موازی با بردار 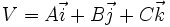 باشد. پس L مجموعه نقاطی است مانند
باشد. پس L مجموعه نقاطی است مانند  به قسمی که بردار
به قسمی که بردار  با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند tt داشته باشیم:
با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند tt داشته باشیم: 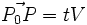 این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از:
این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از: 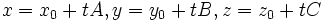
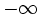 تا
تا 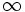 افزایش مییابد نقطه
افزایش مییابد نقطه 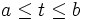 را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود.
را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود. 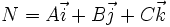 عمود است. پس M از مجموعه نقاطی مانند
عمود است. پس M از مجموعه نقاطی مانند 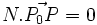
 که بردارهای
که بردارهای  قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود:
قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود: 

