دانلود با لینک مستقیم و پر سرعت .

تعریف دنباله
تابعی را که قلمروش مجموعه اعداد طبیعی و بردش مجموعه غیرتهی A باشد یک دنباله مینامیم. اعداد واقع در برد یک دنباله را جملات دنباله و جمله n ام را با  نمایش داده و جمله عمومی دنباله میگوئیم. بنابراین اگر تابع f از N به A یک دنباله و
نمایش داده و جمله عمومی دنباله میگوئیم. بنابراین اگر تابع f از N به A یک دنباله و  و مقدار f به ازای n باشد مینویسیم.
و مقدار f به ازای n باشد مینویسیم. 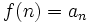 . یک دنباله را بصورت
. یک دنباله را بصورت 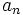 نمایش میدهند.
نمایش میدهند.
نکته
اگر A=R یا A=Q باشد آنگاه f را بترتیب دنباله حقیقی یا دنباله مختلط مینامیم.
تعریف
الف) دنباله 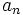 صعودی (نزولی) نامیده میشود اگر به ازای
صعودی (نزولی) نامیده میشود اگر به ازای  داشته باشیم:
داشته باشیم:
ب) دنباله 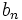 ناصعودی (نانزولی) نامیده میشود اگر به ازای هر
ناصعودی (نانزولی) نامیده میشود اگر به ازای هر  داشته باشیم:
داشته باشیم:
پ) دنباله حقیقی 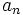 که دارای یکی از ویژگیهای الف یا ب است، دنباله یکنوا نامیده میشود.
که دارای یکی از ویژگیهای الف یا ب است، دنباله یکنوا نامیده میشود.
ت) دنباله حقیقی 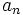 را از بالا (پایین) کراندار مینامند اگر عدد مثبت M وجود داشته باشد که به ازای هر
را از بالا (پایین) کراندار مینامند اگر عدد مثبت M وجود داشته باشد که به ازای هر  داشته باشیم:
داشته باشیم:
ث) دنباله 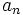 کراندار نامیده میشود اگر هم از بالا و هم از پایین کراندار باشد. دنبالهای که کراندار نباشد بیکران است.
کراندار نامیده میشود اگر هم از بالا و هم از پایین کراندار باشد. دنبالهای که کراندار نباشد بیکران است.
همگرایی و یا عدمهمگرایی دنباله
میگوئیم دنباله عددی 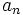 به عدد L همگراست اگر به ازای هر
به عدد L همگراست اگر به ازای هر 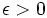 عدد طبیعی N وجود داشته باشد که:
عدد طبیعی N وجود داشته باشد که:
بعبارت بهتر دنباله فوق به عدد L همگرا است اگر به ازای هر 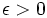 از مرحلهای به بعد تمام جملههای آن در
از مرحلهای به بعد تمام جملههای آن در 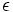 همسایگی L قرار گیرند. دنبالهای که به عددی همگرا نباشد. واگرا نامیده میشود. در حقیقت همگرایی دنباله
همسایگی L قرار گیرند. دنبالهای که به عددی همگرا نباشد. واگرا نامیده میشود. در حقیقت همگرایی دنباله 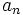 به عدم L همارز تعریف عدد LL بعنوان حد در بینهایت تابعی است که دنباله را تعریف میکند و چون حد تابع در هر نقطه منحصر بفرد است. پس L یکتاست.
به عدم L همارز تعریف عدد LL بعنوان حد در بینهایت تابعی است که دنباله را تعریف میکند و چون حد تابع در هر نقطه منحصر بفرد است. پس L یکتاست.
سوالی که مطرح میشود این است که چه نوع دنبالههایی همگرا هستند؟
در پاسخ به سوال فوق قضیه مهم زیر را داریم:
قضیه
هر دنباله یکنوا و کراندار همگراست. از مهمترین ویژگیهای دنبالههای همگرا کرانداربودن آنهاست. بنابراین دنبالههای همگرا زیردستهای از دسته دنبالههای کراندار هستند. عکس این مطلب صحیح نیست یعنی دسته دنبالههای کراندار زیردسته دنبالههای همگرا نیست. با توجه به مطالب ذکر شده نتیجه مهم دیگری که میگیریم این است که: هر دنباله همگرا کراندار است. اما ممکن است دنبالهای کراندار باشد ولی همگرا نباشد مثل دنباله  با اینکه کراندار است ولی واگراست. توجه میکنیم که در کاربرد قضیه ذکر شده در بالا باید هر دو شرط یکنوایی و کرانداری همزمان برقرار باشد تا نتیجه بگیریم دنباله همگراست. در مثال ذکر شده دنباله یکنوا نیست زیرا به ازای nهای مثبت پاسخ مثبت 1 میشود و به ازای nهای فرد پاسخ منفی یک خواهد بود پس یکنوا نیست بلکه نوسانی است بنابراین حد ندارد در نتیجه واگراست.
با اینکه کراندار است ولی واگراست. توجه میکنیم که در کاربرد قضیه ذکر شده در بالا باید هر دو شرط یکنوایی و کرانداری همزمان برقرار باشد تا نتیجه بگیریم دنباله همگراست. در مثال ذکر شده دنباله یکنوا نیست زیرا به ازای nهای مثبت پاسخ مثبت 1 میشود و به ازای nهای فرد پاسخ منفی یک خواهد بود پس یکنوا نیست بلکه نوسانی است بنابراین حد ندارد در نتیجه واگراست.
نکته
دنبالههای ثابت همگرا هستند یعنی اگر k عدد ثابت دلخواهی باشد آنگاه دنباله ثابت  که به ازای هر n با
که به ازای هر n با 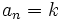 تعریف شده است همگرا به k میباشد.
تعریف شده است همگرا به k میباشد.
دنبالههای کشی
دنباله 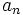 را کشی گویند اگر به ازای هر
را کشی گویند اگر به ازای هر 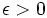 عدد طبیعی N وجود داشته باشد که
عدد طبیعی N وجود داشته باشد که
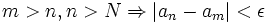 نکته بسیار مهم درباره دنبالههای کشی این است که هر دنباله کشی همگراست. عکس این مطلب نیز صحیح است یعنی هر دنباله کشی همگراست. این مطلب را بدون اثبات میپذیریم.
نکته بسیار مهم درباره دنبالههای کشی این است که هر دنباله کشی همگراست. عکس این مطلب نیز صحیح است یعنی هر دنباله کشی همگراست. این مطلب را بدون اثبات میپذیریم.
در مورد دنبالهها لازم است بدانیم که
- هرگاه دنبالههای
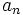 و
و 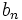 به ترتیب به B , A همگرا باشند آنگاه مجموع دو دنباله به
به ترتیب به B , A همگرا باشند آنگاه مجموع دو دنباله به  همگرا است. ضرب دو دنباله فوق در یکدیگر به
همگرا است. ضرب دو دنباله فوق در یکدیگر به  همگراست. حاصل تقسیم دو دنباله ذکر شده به
همگراست. حاصل تقسیم دو دنباله ذکر شده به 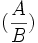 همگراست مشروط بر اینکه
همگراست مشروط بر اینکه 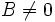 و
و  هرگز صفر نباشد. هرگاه kk یک عدد ثابت و دلخواه باشد در اینصورت
هرگز صفر نباشد. هرگاه kk یک عدد ثابت و دلخواه باشد در اینصورت  فرض است که جمیع حدود به ازای n بسمت بینهایت گرفته میشوند.
فرض است که جمیع حدود به ازای n بسمت بینهایت گرفته میشوند.
نتیجه
هرگاه دنباله 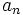 واگرا بوده و C عددی مخالف صفر باشد آنگاه دنباله
واگرا بوده و C عددی مخالف صفر باشد آنگاه دنباله 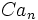 واگرا میباشد.
واگرا میباشد.
قضیه ساندویچ
هرگاه به ازای هر n بزرگتر از اندیسی چون N  و
و 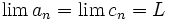 آنگاه نیز
آنگاه نیز 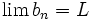 خواهد بود. کاربرد مطالب فوق توسط قضیهای وسیع میشود که میگوید حاصل اعمال یک تابع پیوسته بر یک دنباله واگرا ، دنبالههای همگراست.
خواهد بود. کاربرد مطالب فوق توسط قضیهای وسیع میشود که میگوید حاصل اعمال یک تابع پیوسته بر یک دنباله واگرا ، دنبالههای همگراست.
قضیه
هرگاه  به L میل کند و تابع f در L پیوسته باشد و در جمیع
به L میل کند و تابع f در L پیوسته باشد و در جمیع  ها تعریف شده باشد آنگاه:
ها تعریف شده باشد آنگاه:
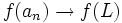
سریها
شرکتپذیری عمل جمع روی مجموعه اعداد حقیقی (مختلط) موجب میشود که مجموعهای متناهی بصورت 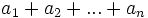 دارای معنی بوده و بدون ابهام باشند. در این قسمت میخواهیم تعداد متناهی عدد را به تعداد نامتناهی عدد تعمیم دهیم.
دارای معنی بوده و بدون ابهام باشند. در این قسمت میخواهیم تعداد متناهی عدد را به تعداد نامتناهی عدد تعمیم دهیم.
تعریف
دنباله 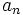 را درنظر بگیرید دنباله جدید
را درنظر بگیرید دنباله جدید 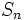 را بصورت زیر تعریف میکنیم:
را بصورت زیر تعریف میکنیم:
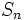 را یک سری مینامیم و آن را
را یک سری مینامیم و آن را 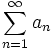 نشان میدهیم و میخوانیم "سری سیگمای
نشان میدهیم و میخوانیم "سری سیگمای  ".
".  را جمله عمومی سری و
را جمله عمومی سری و  را مجموع جزئی nام آن میگوئیم. توجه کنید که
را مجموع جزئی nام آن میگوئیم. توجه کنید که  مجموع n جمله اول سری است و به اینکه n از صفر یا 1 و یا هر عدد دیگری شروع شده باشد بستگی ندارد.
مجموع n جمله اول سری است و به اینکه n از صفر یا 1 و یا هر عدد دیگری شروع شده باشد بستگی ندارد.
همگرایی و عدمهمگرایی سریها
سری 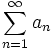 را همگرا گوئیم در صورتی که دنباله مجموعهای جزئی آن همگرا باشد. در غیر اینصورت واگرا نامیده میشود.
را همگرا گوئیم در صورتی که دنباله مجموعهای جزئی آن همگرا باشد. در غیر اینصورت واگرا نامیده میشود.
شرط کشی برای همگرایی سریها
سری 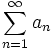 همگراست اگر و تنها اگر به ازای هر
همگراست اگر و تنها اگر به ازای هر 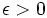 عدد طبیعی N باشد که به ازای هر عدد طبیعی n>N و هر عدد طبیعی P داشته باشیم:
عدد طبیعی N باشد که به ازای هر عدد طبیعی n>N و هر عدد طبیعی P داشته باشیم:
این شرط را شرط کشی برای همگرایی سریها مینامند. نتیجه این که اگر سری فوق همگرا باشد آنگاه:
در صورتی که حد فوق مخالف صفر باشد آنگاه سری واگراست. توجه میکنیم که از قاعده فوق بیشتر برای اثبات واگرایی سریها استفاده میشود زیرا ممکن است حد جمله عمومی برابر صفر باشد ولی سری همگرا نباشد مثل سری موزون 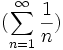 با اینکه حد جمله عمومیاش برابر صفر است ولی واگراست. بنابراین در مورد حد فوق تنها مطلب و نتیجه قطعی که میتوان گرفت این مساله است که اگر حد مخالف صفر باشد بطور قطع سری واگراست ولی اگر مساوی صفر شد نمیتوان نتیجهای گرفت و باید از آزمونهای مناسب دیگری یاری جست.
با اینکه حد جمله عمومیاش برابر صفر است ولی واگراست. بنابراین در مورد حد فوق تنها مطلب و نتیجه قطعی که میتوان گرفت این مساله است که اگر حد مخالف صفر باشد بطور قطع سری واگراست ولی اگر مساوی صفر شد نمیتوان نتیجهای گرفت و باید از آزمونهای مناسب دیگری یاری جست.
با توجه به آنچه که تاکنون در مورد سریها ذکر شد باید متوجه شده باشید که تعیین همگرایی یا واگرایی یک سری از هدفهای مهم مطالعه سریهاست. برای تعیین همگرایی یا واگرایی سریهای با جملههای حقیقی (مختلط) مطالعه سریهایی که جملههای آنها دارای ویژگیهای خاصی هستند اهمیت فراوانی دارد از جمله این سریها ، سریهای متناوب ، سریهای تلسکوپی و سریهای با جملههای مثبت هستند.
تعریف سری متناوب
سری 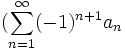 را که در آن
را که در آن 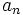 دنبالهای جملههای مثبت ، نزولی و همگرا به صفر است یک سری متناوب نامیده میشود.
دنبالهای جملههای مثبت ، نزولی و همگرا به صفر است یک سری متناوب نامیده میشود.
تعریف سری تلسکوپی
اگر دنبالههای 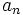 و
و 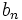 توسط رابطه
توسط رابطه  بهم مربوط باشند. و اگر
بهم مربوط باشند. و اگر 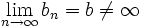 وجود داشته باشد آنگاه سری
وجود داشته باشد آنگاه سری 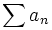 که سری تلسکوپی نامیده میشود همگراست و داریم:
که سری تلسکوپی نامیده میشود همگراست و داریم:
تعریف سریهای با جملههای مثبت
اگر تمام جملههای دنباله 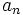 نامنفی باشند آنگاه سری
نامنفی باشند آنگاه سری 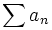 یک سری با جملات مثبت نامیده میشود.
یک سری با جملات مثبت نامیده میشود.
آزمونهایی که برای تعیین همگرایی و واگرایی سریها مورد استفاده است
آزمون مقایسه
سریهای با جملههای نامنفی 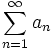 و
و  را درنظر میگیریم:
را درنظر میگیریم:
الف) اگر به ازای هر عدد طبیعی n ، 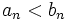 باشد و اگر
باشد و اگر  همگرا باشد آنگاه سری
همگرا باشد آنگاه سری 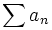 نیز همگراست.
نیز همگراست.
ب) اگر به ازای هر عدد طبیعی n ، 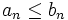 و
و 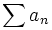 واگرا باشد آنگاه سری
واگرا باشد آنگاه سری  نیز واگراست.
نیز واگراست.
آزمون مقایسه از نظر علمی این کاستی را دارد که بدون اطلاع از نوع برخی سریها نمیتوان نوع برخی دیگر را تعیین کرد.
آزمون نسبت یا قاعده دالامبر
اگر به ازای هر n ،  و
و 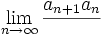 موجود و مساوی a باشد آنگاه:
موجود و مساوی a باشد آنگاه:
الف) اگر a<1 آنگاه سری همگراست.
ب) اگر a>1 آنگاه سری واگراست.
ج) اگر a=1 نتیجه ای نمیتوان گرفت.
از این آزمون برای سریهایی که دنباله آنها بصورت فاکتوریل و یا توانی است میتوان استفاده کرد.
آزمون ریشه
اگر به ازای هر عدد طبیعی n ،  و
و 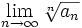 وجود داشته و مساوی L باشد آنگاه:
وجود داشته و مساوی L باشد آنگاه:
الف) سری همگراست اگر L<1 باشد.
ب) سری واگراست اگر L>1 باشد.
ج) نتیجهای نمیتوان گرفت اگر L=1 باشد.
آزمون انتگرال
تابع f با ویژگیهای زیر را درنظر بگیرید:
الف) f روی مجموعه 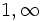 تعریف شده، پیوسته و مثبت است.
تعریف شده، پیوسته و مثبت است.
ب) به ازای هر 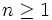 و
و 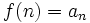 .
.
پ) f نزولی است و داریم: n ،  و
و  .
.
در اینصورت نوع سری 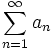 و نوع انتگرال
و نوع انتگرال 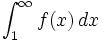 یکی است. یعنی شرط لازم و کافی برای همگرایی سری ذکر شده همگرایی انتگرال فوق است.
یکی است. یعنی شرط لازم و کافی برای همگرایی سری ذکر شده همگرایی انتگرال فوق است.
فهرست مطالب:
دنباله
تعریف
مثال
دنباله همگرا
دنباله واگرا
اثبات
مثال
دنباله صعودی
دنباله نزولی
مثال
دنباله کوشی
قواعد محاسبه
مثال
قضیه ساندویچ
مثال
سری
تعریف
مثال
سری همگرا
شرط کوشی برای همگرایی
سری هندسی
جبر سری ها
همگرایی مطلق
همگرایی مشروط
سری متناوب
مثال
آزمون های همگرایی
آزمون مقایسه
مثال
صورت حدی آزمون مقایسه
مثال
آزمون نسبت دالامبر
مثال
آزمون انتگرال
مثال
سری توانی
مثال ها
پیوستگی، مشتق و انتگرال سری توانی
مثال
سری دوجمله ای
مثال
بسط تیلور
بسط مک لورن
مثال
و...




 نمایش داده و جمله عمومی دنباله میگوئیم. بنابراین اگر تابع f از N به A یک دنباله و
نمایش داده و جمله عمومی دنباله میگوئیم. بنابراین اگر تابع f از N به A یک دنباله و 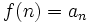 . یک دنباله را بصورت
. یک دنباله را بصورت 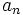 نمایش میدهند.
نمایش میدهند.  داشته باشیم:
داشته باشیم: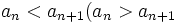
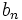 ناصعودی (نانزولی) نامیده میشود اگر به ازای هر
ناصعودی (نانزولی) نامیده میشود اگر به ازای هر 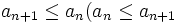
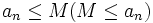
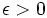 عدد طبیعی N وجود داشته باشد که:
عدد طبیعی N وجود داشته باشد که: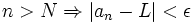
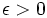 از مرحلهای به بعد تمام جملههای آن در
از مرحلهای به بعد تمام جملههای آن در 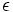 همسایگی L قرار گیرند. دنبالهای که به عددی همگرا نباشد. واگرا نامیده میشود. در حقیقت همگرایی دنباله
همسایگی L قرار گیرند. دنبالهای که به عددی همگرا نباشد. واگرا نامیده میشود. در حقیقت همگرایی دنباله  با اینکه کراندار است ولی واگراست. توجه میکنیم که در کاربرد قضیه ذکر شده در بالا باید هر دو شرط یکنوایی و کرانداری همزمان برقرار باشد تا نتیجه بگیریم دنباله همگراست. در مثال ذکر شده دنباله یکنوا نیست زیرا به ازای nهای مثبت پاسخ مثبت 1 میشود و به ازای nهای فرد پاسخ منفی یک خواهد بود پس یکنوا نیست بلکه نوسانی است بنابراین حد ندارد در نتیجه واگراست.
با اینکه کراندار است ولی واگراست. توجه میکنیم که در کاربرد قضیه ذکر شده در بالا باید هر دو شرط یکنوایی و کرانداری همزمان برقرار باشد تا نتیجه بگیریم دنباله همگراست. در مثال ذکر شده دنباله یکنوا نیست زیرا به ازای nهای مثبت پاسخ مثبت 1 میشود و به ازای nهای فرد پاسخ منفی یک خواهد بود پس یکنوا نیست بلکه نوسانی است بنابراین حد ندارد در نتیجه واگراست.  که به ازای هر n با
که به ازای هر n با 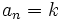 تعریف شده است همگرا به k میباشد.
تعریف شده است همگرا به k میباشد. 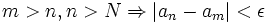 نکته بسیار مهم درباره
نکته بسیار مهم درباره  همگرا است. ضرب دو دنباله فوق در یکدیگر به
همگرا است. ضرب دو دنباله فوق در یکدیگر به  همگراست. حاصل تقسیم دو دنباله ذکر شده به
همگراست. حاصل تقسیم دو دنباله ذکر شده به 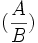 همگراست مشروط بر اینکه
همگراست مشروط بر اینکه 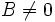 و
و  هرگز صفر نباشد. هرگاه kk یک عدد ثابت و دلخواه باشد در اینصورت
هرگز صفر نباشد. هرگاه kk یک عدد ثابت و دلخواه باشد در اینصورت  فرض است که جمیع حدود به ازای n بسمت بینهایت گرفته میشوند.
فرض است که جمیع حدود به ازای n بسمت بینهایت گرفته میشوند.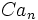 واگرا میباشد.
واگرا میباشد.  و
و 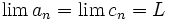 آنگاه نیز
آنگاه نیز 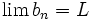 خواهد بود. کاربرد مطالب فوق توسط قضیهای وسیع میشود که میگوید حاصل اعمال یک تابع پیوسته بر یک دنباله واگرا ، دنبالههای همگراست.
خواهد بود. کاربرد مطالب فوق توسط قضیهای وسیع میشود که میگوید حاصل اعمال یک تابع پیوسته بر یک دنباله واگرا ، دنبالههای همگراست. 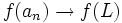
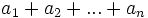 دارای معنی بوده و بدون ابهام باشند. در این قسمت میخواهیم تعداد متناهی عدد را به تعداد نامتناهی عدد تعمیم دهیم.
دارای معنی بوده و بدون ابهام باشند. در این قسمت میخواهیم تعداد متناهی عدد را به تعداد نامتناهی عدد تعمیم دهیم. 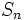 را بصورت زیر تعریف میکنیم:
را بصورت زیر تعریف میکنیم: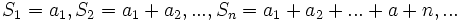
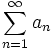 نشان میدهیم و میخوانیم "سری سیگمای
نشان میدهیم و میخوانیم "سری سیگمای  را مجموع جزئی nام آن میگوئیم. توجه کنید که
را مجموع جزئی nام آن میگوئیم. توجه کنید که 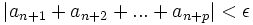
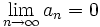
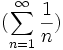 با اینکه حد جمله عمومیاش برابر صفر است ولی واگراست. بنابراین در مورد حد فوق تنها مطلب و نتیجه قطعی که میتوان گرفت این مساله است که اگر حد مخالف صفر باشد بطور قطع سری واگراست ولی اگر مساوی صفر شد نمیتوان نتیجهای گرفت و باید از آزمونهای مناسب دیگری یاری جست.
با اینکه حد جمله عمومیاش برابر صفر است ولی واگراست. بنابراین در مورد حد فوق تنها مطلب و نتیجه قطعی که میتوان گرفت این مساله است که اگر حد مخالف صفر باشد بطور قطع سری واگراست ولی اگر مساوی صفر شد نمیتوان نتیجهای گرفت و باید از آزمونهای مناسب دیگری یاری جست.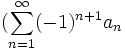 را که در آن
را که در آن  بهم مربوط باشند. و اگر
بهم مربوط باشند. و اگر 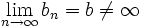 وجود داشته باشد آنگاه سری
وجود داشته باشد آنگاه سری 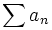 که سری تلسکوپی نامیده میشود همگراست و داریم:
که سری تلسکوپی نامیده میشود همگراست و داریم: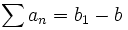
 را درنظر میگیریم:
را درنظر میگیریم: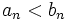 باشد و اگر
باشد و اگر  همگرا باشد آنگاه سری
همگرا باشد آنگاه سری 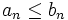 و
و  و
و 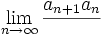 موجود و مساوی a باشد آنگاه:
موجود و مساوی a باشد آنگاه: 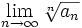 وجود داشته و مساوی L باشد آنگاه:
وجود داشته و مساوی L باشد آنگاه:  تعریف شده، پیوسته و مثبت است.
تعریف شده، پیوسته و مثبت است. 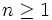 و
و 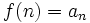 .
.  .
. 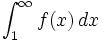 یکی است. یعنی شرط لازم و کافی برای همگرایی سری ذکر شده همگرایی انتگرال فوق است.
یکی است. یعنی شرط لازم و کافی برای همگرایی سری ذکر شده همگرایی انتگرال فوق است.